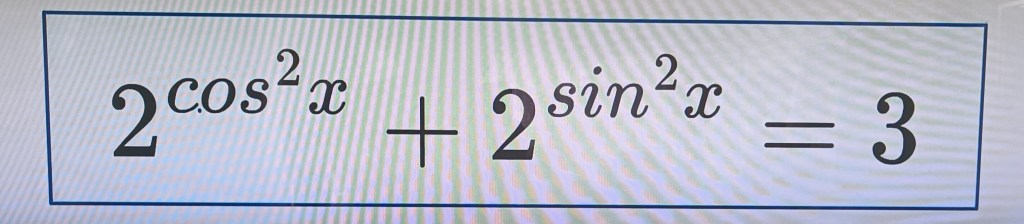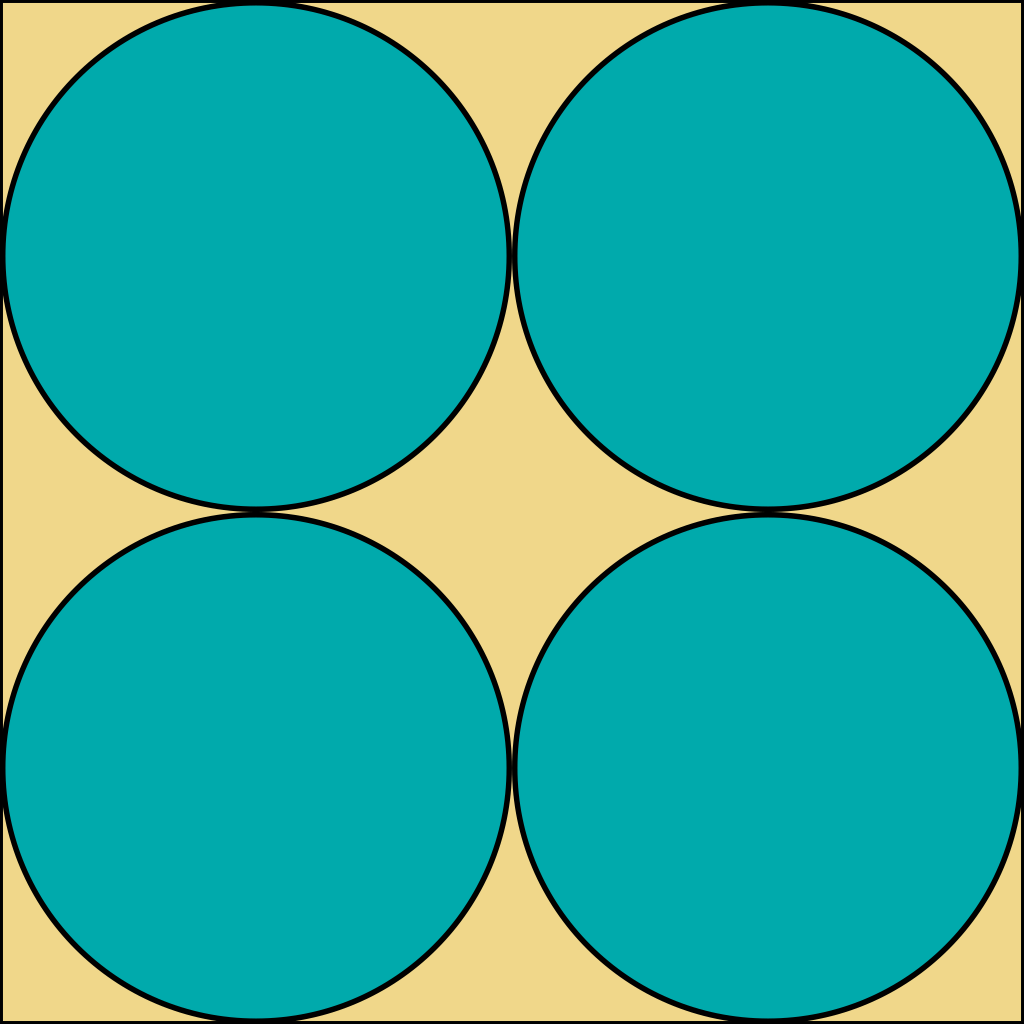Paul Motwani

Blog Post #176: Many Blessings at the World Senior Chess Championship in Italy 🙏

Dear Readers,

I am writing this particular blog post at Verso Oriente 👌, a lovely guest house in Brindisi 😍, Italy. Very early tomorrow morning, I have flights ✈️ back home to Brussels (via Rome). I have been in Italy continuously for slightly more than two weeks already, as I competed in the World Senior 50+ Chess Championship which was held at the Grand Hotel Costa Brada in sunny Gallipoli 🌞.

In total, a record number of more than 430 chess players converged on Gallipoli to take part in the 65+ or 50+ World Senior Championship, for men or women.

Special congratulations 👏🎊🍾 to Scotland’s GM Ketevan Arakhamia-Grant who won the Women’s 50+ Championship with a magnificent score of 8.5/11 🏆. Keti finished ahead of 30 other lady players, and was a full point ahead of GM Pia Cramling & WGM Maritza Robaina Arribas, the respective Silver and Bronze medal winners.

‘Keti’ 🥰 World Senior 50+ Women’s Chess Champion 2025 🏆🙌

Out of 154 players in the Open 50+ Championship, there were 153 men and just one woman: Candidate Master Helen Milligan, who currently resides in New Zealand, but comes originally from St. Andrews, Scotland.

Helen and a cute cat! 😻 (Lovely photo seen on Helen’s Facebook page.) 💖

In addition to Helen, there were 8 other Candidate Masters, 21 FIDE Masters, 25 International Masters, and 18 Grandmasters (including myself) among all the players in the super-strong Open 50+ event.

The convincing Gold medal winner was Israeli Grandmaster Victor Mikhalevski with 9.5/11 👏🏆.

As I don’t currently play often (because I am still working hard as a Mathematics teacher at Musica Mundi School in Waterloo, Belgium), the 11 opponents whom I personally played against in Gallipoli were the toughest I have faced in a long time. I played against 5 GMs, 3 IMs, 2 FMs and one currently untitled but dangerous Azerbaijani player.

I thank God for guiding me to a very good result of 7.5/11, comprised of 5 wins, 5 draws, and just one loss (in round 8 of the eleven) 🙏💗.

In the final round, I didn’t quite manage to win against Georgian Grandmaster Mikheil Kekelidze (the Silver medal winner). I had my chances, but it was not my destiny this time.

I am truly grateful, though, to have finished 5th = (7th on tiebreak) in such a long and tough tournament 😊. My personal games were really hard-fought battles, averaging 49 moves and totalling 49 x 11 = 539 moves over the entire event.

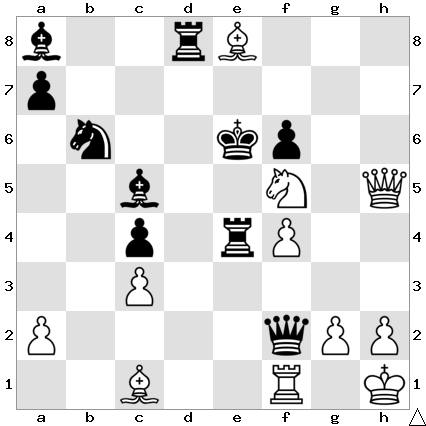
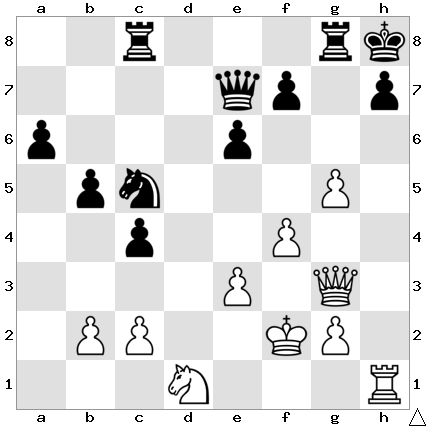
Here comes a nice tactical finish from my shortest game in Gallipoli.

**It’s White to play and win in the game GM P A Motwani vs. GM Alexander Raetsky**
**from round 4 in Gallipoli on 24.10.2025**.

The crisp finish was 1 Rxd4! Nxd4 2 Ba5! Re7 3 Bf1! Nc6 4 Ba6! Kd8 5 Bb5! 1:0. Black resigned in view of 5…Nxa5 6 Rb8#, checkmate.

No-doubt, very many people have personal challenges to bear with at numerous times in their lives. I can say honestly, that (due to ongoing medical difficulties which began way back in 2001), I sometimes struggle with acute physical discomfort during long chess games. The wonderful doctors and nurses at the UZ Hospital in Jette, Belgium (which I go to for a necessary medical procedure every few weeks) do their utmost to help me well 🙏.

If I am still blessed with sufficient health and time in future, then I hope to try again, perhaps in the 65+ section in a couple of years from now. This year, in the 50+ event, I was (now at age 63) one of the oldest players in that group. Energy levels matter a lot in long, tough chess games. I will be trying to improve my physical fitness, as well as endeavouring in some spare time to improve my play in technical positions, in addition to sharpening tactical awareness and deepening my openings knowledge, too. I of course tried my utmost in preparing long before (and during) the event in Gallipoli, but there’s still more good work to be done, and I will ask for the strength to do it 🙏.

In the meantime, I offer deep, sincere thanks to very many people, including family members, dear friends, colleagues, students, organisers and others for their great love, support and encouragement which made my participation in Gallipoli possible and a joy for me 🥰💖.

Every time that I do play Chess, I always remember with love and gratitude the myriad golden tips and gems of wisdom that I received over many years from my late, great friend and mentor, Dundee’s Paul Fitzpatrick (1948-2024) 💗

Here now is a selection of nice recent photos 💖.

Paul, Jenny, Michael & Nicky celebrating Michael’s recent birthday 💖

Kortrijk Chess Club 75th Birthday Celebration, 27.9.2025 🥰

Lots of Friends at the Kortrijk Chess Club 75th Birthday Celebrations on 27.9.2025

Candidate Master Timothy Mifsud from Malta very kindly (on 20 September this year) sent me a gift of his Chess Spider! 4.2 (the most up-to-date version that he has created, so far). You can read about it below, and you can order directly from Tim (at an excellent price) via chessbites@gmail.com. Feel free to also check out his site http://www.chessbites.com 👍.

**Chess Spider! 4.2 by Candidate Master Timothy Mifsud from Malta 👍**

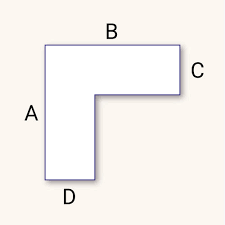
As I’m resuming Maths teaching at the beautiful Musica Mundi School (MMS) on Wednesday morning, 5 November, here now is a Prize Puzzle for all the students and my colleagues to enjoy. It’s specially dedicated to Eric Van Steerteghem, the father of my superb young Maths colleague, Jens Van Steerteghem 🥰.

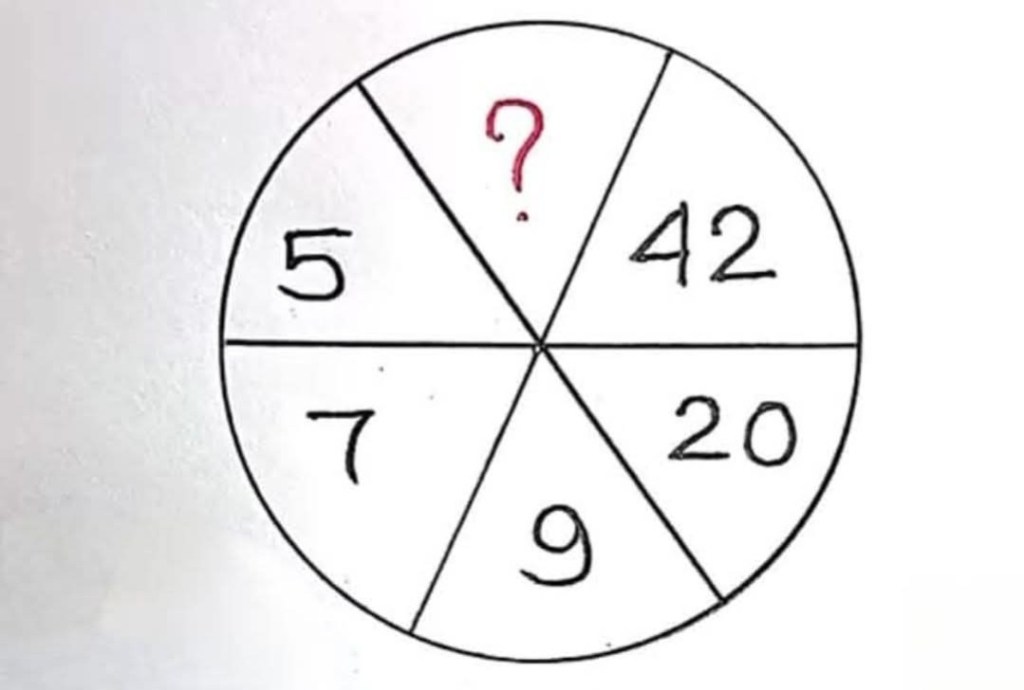
Regarding this fun Prize Puzzle, I’m warmly inviting all students (and colleagues!) at MMS to email me before midnight tomorrow (Tuesday) telling me what the missing number is.

Remember to include a clear reason for your choice!

To conclude this Blog Post #176, we have the beautiful and inspiring Bible passage Luke 17:6. Jesus said, “If you have faith even as small as a mustard seed, you can say to this mulberry tree, ‘Be uprooted and planted in the sea,’ and it will obey you.”

Blog Post #175: Thanks Always For Every Moment 🥰

Dear Readers,

Though it’s been almost four and a half months since my previous published blog post, I don’t forget to give thanks always to God for every moment of every day 🥰

I will now share some of those blessings via a nice selection of happy photos 😊

Beautiful Cherry Blossoms in Tokyo, Japan, in early April 😍

Celebrations with friends and relatives in Tokyo 🥰

20th Wedding Anniversary Celebration in Buggenhout for Patrick & Roberta 🥰

Jenny & I celebrated our Pearl Wedding Anniversary this summer 💕

Geraardsbergen Senior Chess Prizegiving Ceremony, 7 August 2025 😊

Special congratulations to Johan Krijgelmans (centre picture) for playing really fabulous Chess 👍

FM Johan Goormachtigh, Gerard Milort (or GM for short! 😁) and IM Aleksander Alienkin all played excellently, too 👌🥰

Many sincere thanks to Dirk Flamée (pictured above on the right & in photos below) and his wonderful team of expert arbiters and very kind assistants who make the annual tournament always so enjoyable and memorable 🥰

**Marc Bils** (pictured left, above) has been a superb arbiter
at tournaments in Geraardsbergen for 32 years! 👌

It’s Black to play and win beautifully 😍, from a training game that I had a few weeks ago

Another beautiful puzzle that I saw (and solved! 😁) some weeks ago. Enjoy cracking it too! 👍

My youngest niece (in England) is predicted to achieve A* results in all of her A-level subjects. Given her immense talent and super-hard work to make great use of everything,
I think she’ll be smiling a lot when she receives her results tomorrow 😊😊😊
Then she, and other keen Maths enthusiasts, can enjoy solving the
trigonometric exponential equation given above. No calculator is needed at all!

I’m very proud of my AS-Level Maths students at Musica Mundi School (MMS), for they all worked extremely hard and got well-earned, high results too 🙌😊

My IGCSE Maths students at MMS also worked hard, and their results will come from Cambridge next week.

Prayer number 100 from a beautiful book of 1000 prayers
that I bought in England this summer 🥰

A beautiful Bible verse to conclude this Blog Post #175 ❤️

Blog Post #174: A Gift For Dear Colleagues and Students ❤️😊

Dear Readers,

At least seven of my colleagues and students have their birthdays coming very soon, before Easter or just shortly afterwards.

The nice prize puzzles in this blog post are dedicated to Raphaël, Seinel, Wout, Louis, Romeo, Simon and Alisa, and of course I wish all readers a really blessed, happy Easter, soon❤️

Imagine that my Musica Mundi School (MMS) excellent Maths colleague, Jens, gives positive whole numbers (one each, in order of increasing size) to Raphaël, Seinel, Wout, Louis, Romeo, Simon and Alisa. Note well: Just two people receive exactly the same number as each other; everyone else gets different, distinct numbers.

The seven numbers given by Jens are special because their Mean, Median, Mode and Range are all exactly equal to seven 👌😊

The image below does NOT show the actual numbers given by Jens! However, it does provide quite a helpful reminder regarding the mathematical meanings of Mean, Median, Mode and Range 👍

Fun Puzzle

Part 1: The first part of this fun puzzle is for you to figure out the numbers that could have been given by Jens to Raphaël, Seinel, Wout, Louis, Romeo, Simon and Alisa.😊

Consider: What is the minimum possible number that could have been given to Raphaël?

Also, what is the maximum possible number that could have been given to Raphaël?

Part 2: Instead, now suppose that the Mean, Median, Mode and Range are all still equal to seven, but more than two people receive the same number as each other. Your fresh challenge is to figure out the numbers that could have been given this time to Raphaël, Seinel, Wout, Louis, Romeo, Simon and Alisa. Enjoy investigating the possibilities! 🙌

At the school, I recently shared an algebra brainteaser which involved solving equations of the type A + 2AB + B = N, where N is a positive whole number and A & B are integers. Jens worked on it with great passion, and succeeded in rearranging the equation to an equivalent form that I had in mind when sending the brainteaser: (2A+1)(2B+1)=2N+1. The brainteaser is then actually simplified and is reduced to finding factors (positive or negative ones) of 2N+1, and equating appropriate factor pairs to 2A+1 & 2B+1. Then you only have to solve straightforward linear equations to figure out the possible values for A & B.

Jens and his father, Eric, love a really good, meaty Maths brainteaser! 😍 So do some very keen students, including Wout, Raphaël and others!

Here comes a fresh, brand-new, original brainteaser…😁

BRAINTEASER 😊😊😊

Part 1

Jens, Wout and Raphaël go into a secret Maths chamber, where three positive numbers are lying on a table. They each take one of the numbers.

Raphaël multiplies his number by the sum of the other two numbers, and gets the correct result, namely 5.

Wout multiplies his number by the sum of the other two numbers, and also gets the correct result, namely 6.

Jens multiplies his number by the sum of the other two numbers, and of course gets the correct result, namely 7.

They announce their results of 5, 6 & 7 to Paul, and challenge Paul to figure out the exact product of (multiplying together) the three numbers that were lying on the table in the secret Maths chamber.

What answer should Paul get for that product?

Part 2

Jens, Wout and Raphaël go back into the secret Maths chamber, where they find three new, positive numbers on the table. They repeat the same type of calculations as they did the first time. Coincidentally, their three results end up being consecutive positive whole numbers again (though not necessarily 5, 6 & 7 this time).

They announce their results to Paul again, and again ask him to figure out the product of the three numbers that were on the table. Please assume that Paul is on good form, and he figures out the product correctly! 😊

What is the probability that Paul’s answer will be a whole number?

You are, as usual, very welcome to send me by email your answers to some or all of the goodies, if you would like to do so 👍💚😊

As always, I thank God with all my heart for giving me a wonderful family, very dear friends, colleagues & students, and for also giving all the beautiful puzzle ideas in their & His honour 💕

I will conclude this blog post with the following lovely Bible verse from John 17:4

“Lord, I have brought You glory on earth by completing the work You gave me to do.”

Blog Post #173: For super Susanna😊and her whole delightful family ❤️

You can’t afford to close your eyes when playing Chess with Super Susanna
because she’s smart and sneaky!! 😁
Benjamin, Tabitha, Joseph and all of Susanna’s siblings have great talents too ❤️

Eyes closed at a Belgian Chess tournament prizegiving ceremony a few days ago was permissible…
because I didn’t have to play Susanna then!! 🤣😂

James & Paul are two of my kindest friends.
Amigos para siempre = Spanish for “Friends Forever”😊😊

James’ wife, Eliane, invited me to their home yesterday evening in early celebration of James’ birthday which is coming up shortly. So is the birthday of James & Eliane’s youngest child…Super Susanna! 😁

For other readers to enjoy as well, I now offer the following original, fresh puzzle in honour of the whole delightful family ❤️

Fun Puzzle starring Jolly James 😁 and Super Susanna 💕

Here are the key facts (in which S, N & A represent positive whole numbers) :-

James’ birthday is in N days from now.

On her birthday N years ago, Susanna turned N cubed years old.

The very next year, Susanna turned S squared years old.

On her birthday exactly N weeks from today, Susanna will be A years old.

On his birthday this year, James’ new age will be exactly equal to the sum 1+2+…+A.

You don’t have to be anywhere near as talented in Mathematics as Benjamin (who’s adjacent to me in the very first photo (see above) in this blog post) in order to now solve these puzzle questions…

What is Susanna’s exact date of birth?
What is James’ exact date of birth?

As always, I thank God with all my heart for giving me such wonderful, dear friends, and for also giving all the beautiful puzzle ideas in their & His honour 💕

I will conclude this blog post with the following important Bible verse from John 17:3

“This is eternal life, that they may know You, the only true God, and Jesus Christ whom You have sent.”

Blog Post #172: Green Secret of the Heartland 💚

Dear Readers,

I have the pleasure of teaching Mathematics at Musica Mundi School (MMS) in Waterloo, Belgium. Today’s blog post is dedicated to Kate and Helen, two great colleagues whose birthdays are coming up very soon during the next school holiday break. The ladies collaborate excellently in their teaching of Global Perspectives, for example, and they are both very skilled in English language work, too, and so I think that they’ll enjoy the following anagram tribute in their honour. The 28 letters in FOR GREAT TEACHERS KATE AND HELEN rearrange perfectly to make AKA GREEN SECRET OF THE HEARTLAND 💚

Bible Psalm 17:2
‘Let my sentence come forth from Thy presence; let Thine eyes behold the things that are equal.’

I thank God with all my heart for giving all the ideas contained in fresh, brand-new prize brainteasers here, which are certainly among my absolute favourites from my life, so far.

💚A Fresh ‘1970s’ Brainteaser In Honour of Kate and Helen 💚

Imagine that the total number of pages in a beautiful, big Global Perspectives book is N, a three-digit whole number in which all three digits are positive and different from each other. By rearranging the order of the digits in N, Kate is able to form five new, different three-digit whole numbers. Helen adds up Kate’s five new numbers and correctly finds that the total sum is Y, a year in the 1970s. That is, Y is a whole number somewhere between 1970 up to not more than 1979.

Your special brainteaser is to figure out, with proof, the exact value of N and the exact value of Y.

Note that this is a very precise mathematical brainteaser. There is no random guesswork involved, and though calculators may be used, they are not strictly required.

Anyone who knows me well, knows that 3 is my absolute favourite number of all 😊😊😊! So, I’m more than happy to now celebrate one other upcoming MMS birthday, in addition to those of Kate and Helen! Next Friday will be the birthday of Lovely Lara, a Hungarian student at the school.

💚 A Fresh L-shape Brainteaser in Honour of Lovely Lara 💚

The image shows an inverted L-shape. Each line of the shape is either horizontal or vertical, just as you would expect from the appearance of the diagram. Assume that all the lengths of the lines are exact whole numbers of centimetres. However, note well that the diagram is certainly NOT drawn to scale!

Now, have a look at the horizontal line going across from the bottom of the side marked C. Imagine extending the left-end point of it with a dotted horizontal line to meet the side marked A. Also from the same left-end point, draw a dotted vertical line upwards to meet the side marked B. You may be wondering whether the wee shape that you’ve now formed in the top left area of the L-shape is a square… Well, yes, I’m declaring now that it is indeed a square!

You are now also told that the total area of the L-shape is L square centimetres, and the total outer perimeter is P centimetres (of course, don’t count any inner “dotted lines” described earlier as part of P; only count the outer perimeter of the L-shape).

Another super-important fact is: you are now given that L = P.

Your brainteaser in honour of Lovely Lara is to figure out, with proof, the exact value of L.

You are always very welcome to send me by email your answers to some or all of the goodies, if you would like to do so 👍💚😊

I will round off here with the beautiful Bible verse Matthew 17:2 ‘There He was transfigured before them. His face shone like the sun, and His clothes became as white as the light.’

Blog Post #171: A Noble Arc ❤️

Dear Readers,

Welcoming archways in Heaven will be infinitely more beautiful than anything we can imagine or have seen so far.

Every time that someone is saved is a reason for great celebration in Heaven.
None of us need miss out on the everlasting joy of God’s Kingdom.
We are all warmly invited. ❤️
Will you accept?

Why not decide to happily answer “YES” in your heart right now (if you haven’t yet done so)? ❤️

I also gratefully thank God for giving the beautiful ideas for all the puzzles and brainteasers in this (and indeed every) blog post. You are always very welcome to send me by email your answers to some or all of the goodies, if you would like to do so 👍❤️

The Loving Living Spirit Equation 💕

L + S + L * S = L² + S² + 1

The above equation is my absolute favourite one ❤️

Given that God’s Love and Spirit are real and are represented here by L and S, my favourite brainteaser for you is to solve (with proof) the equation

L + S + L * S = L² + S² + 1

Puzzle to Celebrate a Lovely Couple 💕

Here in Blog Post #171, think of the largest prime divisor (or factor) of 171. The correct prime factor (19) is the number of years that Patrick & Roberta have been married, and they’re planning a wonderful summer feast later this year to celebrate their 20th wedding anniversary 💕

Roberta & Patrick will soon be celebrating their ‘China’ wedding anniversary = 20 years 💕

Suppose that P, R & I represent three different prime numbers, and I + R = P. Also, R + R – I = 20.

To discover the day number and month when my wife (Jenny) and I are going to celebrate with Patrick & Roberta, figure out the exact value of P * R * I * I ÷ 20.

Puzzles in Honour of Students 👍😊

Imagine a mathematical student saying to me, “Mr. Mo, I’m thinking of a particular year _ _ _ _ from within the time of your life so far. If I insert my favourite one-digit number in the middle, to get _ _ _ _ _ , then the resulting number equals the cube of my house number !”

Your fun challenge is to figure out both the student’s favourite one-digit number and the house number 😁.

Warm Welcome to Anna K. Puzzle 😍

Anna K. is the newest student who arrived at Musica Mundi School (MMS) just a few days ago. It’s lovely that she’s featuring here in Blog Post #171, because Anna’s birthday is actually 20 June = day number 171 of the year! This year, she’ll be turning from 16 to 17.

(16 + 17) * FUN = 20FUN

where FUN represents a certain three-digit number and 20FUN represents a five-digit number.

Your FUN puzzle is to figure out the exact value of FUN.

B😊NUS PUZZLE

I’m now thinking of three particular, consecutive prime numbers. The total sum of their squares equals 3171.

Your fun bonus challenge is to figure out exactly which three prime numbers I’m thinking of.

Happy Valentin’s Day Puzzle!! 😁

Today, 25.1.25, is the 25th day of the year, and also the birthday of Valentin, one of my Mathematics students at MMS. In HH days from now (where HH represents a particular two-digit number), it will be day number XY of this year, where XY represents a rather special two-digit number. A delightful detail is the fact that XY days is actually equal to X days + Y weeks 😊

Your fun puzzle challenge is to figure out the exact values of H, X and Y.

A FAV Puzzle 😍 (in honour of students Faye and Artemii (& Valentin of course) whose birthdays are coming up within the next couple of days).

Faye, Artemii and Valentin know that 3 is my absolute favourite number, but I also like square numbers. So, imagine that they discover the smallest positive whole number W for which W squared begins with three 3s (on the left).

The fresh fun challenge is to discover the exact value of W 👌😊.

A Circular Cakes & Cream Brainteaser 👌😍

I couldn’t help imagining delicious cakes and cream when looking at the diagram of 4 identical circles set up nicely on a square tray 😁!

Your tasty brainteaser is to figure out (correct to 4 significant figures) the area of the central yellow part as a percentage of the area of the entire square.

Extra-special congratulations if you can prove mathematically that your answers up to here in this blog post are the correct solutions to the two brainteasers and six number puzzles presented so far.

A Knight’s Tale about King Richard! 🤣😂

A very nice photo from last October.
Richard is one of the keenest students who loves to play at the Musica Mundi School Chess Club😊.

Last week, just for fun, Richard sneakily moved a queen like a knight in order to turn a ‘checkmate in two moves’ puzzle into an immediate mate in one move!! Everyone there (myself included) had a good laugh about it!

Now, though, I’m making sure to present a puzzle position involving a real knight but no queen! 😂

It’s a delightful puzzle that I saw posted recently on Facebook.

It’s White to play and force checkmate in not more than six moves! 😍

Word Puzzle: Rearrange the letters of A NOBLE ARC to make the name of a very well-known, stunning city beginning with B.

I may visit beautiful Barcelona some day…
but Heaven is where I want to live forever
and it’s free for everyone who recognises
and gratefully accepts God’s gift.❤️

Let’s enjoy an extra double bonus brainteaser treat before wrapping up this blog post!! 🙌😊

Two friends share the same birthday (25 January), but their ages are several years apart. Today, the younger friend said to the older one: “When I reach the age that you are now, the product of our ages then will be very nearly 200 more than the product of our ages now.”

This modest brainteaser/puzzle is for you to figure out (with proof) the exact dates of birth of the two friends.

In a particular family, the father is several years older than his wife. Let’s call their age difference N. They also have N children. One great grandfather is still alive, and he helps to make Maths homework easier for everyone! 👍😁

The product that would result from multiplying together N by the ages of the great grandfather, the father, and his wife, would of course be a large number, but curiously it would only involve one particular digit repeated all the way from the start, left-end of the number to the finish, right-end of the number.

Your Brainteaser Challenge is to figure out the value of N, and also the ages of the great grandfather, the father, and his wife.

To finish, here is a beautiful quote from John 17:1 in The Bible:

After Jesus had spoken these words, He looked up to Heaven and said, ‘Father, the hour has come; glorify your Son so that the Son may glorify You.’

Blog Post #170: Now Is The Time; Best Groningen Chess 👍😊❤️

Dear Readers,

Let’s begin with a quick, wee warm-up of three checkmate puzzles in 3, 3 or 3+3 moves based on a trio of actual games from…1925 ! 😁

Checkmate Puzzle Solutions

A) 1 Qf7+! Kxf5 2 g4+ Kxg4 3 Qh5#

B) 1 Rxe6! leaves Black with nothing better than 1…Rff7 2 Bxg7+! Rxg7 3 Re8#

C) 1 Rxh7+! Kxh7 2 Qh3+ Kg6 3 Qh6+ Kf5 4 Qh7+! Kg4 5 Qh3# or 4…Rg6 5 Qh3+ Ke4 6 Nc3#

The multiple purposes of this article include:- most sincerely wishing everyone a very blessed, happy New Year; writing about a wonderfully-organised international Chess festival which concluded on December 30 in Groningen in the North of The Netherlands; sharing some good fun freshly-created puzzles (involving Chess, Mathematics and more); sharing a vitally-important reflection which I honestly know more about, with certainty, than anything else I know. Indeed, it’s the duty of everyone who knows the Good News to share it with others, in the hope that they will come to love, respect and accept with gratitude to God the priceless gift which He offers freely to everyone. Peoples’ individual decisions to accept the gift (or not) will be of eternal importance, so it’s not something to ignore or delay.

❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️

A lovely Chess for Peace 💕 card given to me previously by Erik van de Wynkele

Since the age of 11, I have enjoyed taking part in nice Chess events during some of my ‘free’ time. Currently, I play competitive Chess only during school holidays, because throughout term times I dedicate a lot of time and energy to giving the highest quality of Mathematics teaching that I can for all of my students. Also, time with family and time to rest well is always important.

I am grateful to Mr. Govert Pellikaan and his fantastic team of organisers & arbiters who made the splendid Groningen Chess Festival run really smoothly for the enjoyment of around 400 people who took part. Meeting so many friendly people was a great pleasure.

Photos by Harry Gielen. Pictured above is the team of arbiters.

Many participants chose for one of the 9-round Open sections, while some others opted for a 4-player, 3-round, all-play-all mini-group. Yet others (including myself) were more than happy with the possibility of playing in a compact 5-round event starting on Boxing Day (26 December). Whichever event one chooses for, it’s highly appealing that its schedule requires just one game per day.

Everyone plays together in a lovely, spacious hall. Drinks, snacks and meals are readily available within the analysis room of the same building, at good prices.

A superb Chess bookstall is provided by Robert Klomp and his wife, WGM Erika Sziva, whose website is http://www.debestezet.nl 👍❤️ The thriving business was founded in 1994.

I was delighted to win the Senior Tournament with 5/5, and the next day my wife (Jenny) and I celebrated New Year’s Eve at the home of Robert & Erika in the Dutch town of Best, where we stayed until the evening of New Year’s Day—a favourite, long-standing tradition with our families 😊😊

A typically stunning photo 😍 by Erika, who is extremely talented.

We all tried to remain well-balanced!! 🤣😂

Jenny & I celebrating the New Year in The Netherlands 💕

We named this photo ‘Orange Peace’ 😊
Orange is a national colour in The Netherlands.

Imagine a great Chess board with its unit squares numbered from 1 to 64.
Jenny and I have gone a long way to reach number 63, with some special thoughts in mind…
for bringing you six threes with a sneaky, fun twist!
Think of the year 1925, from a century ago. Reverse its digits to get 5291.
Multiply by 63, and the result is a super six-digit string 333333
consisting entirely of 3s; my absolute favourite! 😁

Question: How can you use the numbers 100, 64, 3 and my house-number 11 to get 21.12, to remind you of December 21, the date when the annual Groningen Chess Festival begins?

Answer: 64 x 3 x 11 ÷ 100 = 21.12 👍😁

Word Puzzle: Can you read my mind and rearrange the 18 letters of CONGRESS BEGINS THEN to make 3 other very particular words!?

Answer: I was thinking of

CONGRESS BEGINS THEN =

BEST GRONINGEN CHESS 👍😊❤️

Nice Number Puzzle: Why is today, 3.1.25, a nice day for me to gratefully celebrate a 5/5 result?

Me with International Master Vadim Cernov,
who was the runner-up on 4/5 in the Senior Tournament.

Answer: 5 to the power of 5 equals 3125 🙌😁

IM Arthur De Winter, WGM Machteld Van Foreest (who achieved an IM norm—warm congratulations! 👍😊), GM S.L.Naranyan, IM Theo Stijve, IM Anto Cristiano F Manish
and GM Thomas Beersden were 6 of the top 7 prizewinners in the Open A-Group.
IM Nick Maatman would also have been pictured, but he had had to leave, sick.

Given that 17-year-old Machteld Van Foreest is a local player from Groningen, her IM norm achievement was a particularly popular result. Today, I have been enjoying playing through some of Machteld’s earlier victories from 2024. I have chosen the following position from the Dutch League, in which it was Machteld as White to play and win by force…and she did so! 😁

The game ended crisply with 1 Re6! Qg5 2 f4! 1-0. Black resigned in view of 2…Qh4 3 Rh6#. It’s true that 1…Qh7 would have been more tenacious, but White would still have won comfortably with 2 Qf4!, intending 2…Rxd5 3 Rh6.

Literally hundreds of great photos were taken by Bart Beijer and Harry Gielen at the tournament. Though I can’t feature all of them here, I do want to congratulate most sincerely every person who was there in Groningen, for everyone’s presence contributed to making an unforgettable event 💕

It was especially nice for me to see Mr. Johan Zwanepol, who was the main organiser when I previously played in Groningen in 1979, 1980, 1989 and 1990 😊

Mr. Johan Zwanepol presenting the Open A-Group Winner’s Trophy to Indian GM S. L. Naranyan 👌😊❤️

13-year-old Scottish super-talent Rishi Vijayakumar very nearly achieved an IM norm.
He still deserves ’10/10′ for excellent, courageous play.
Rishi loves Maths, too. So, here comes a nice puzzle in his honour…

Without needing to use a calculator or any other external aids, can you figure out mentally the exact value of the square root of (1+3+5+…+2023+2025)?

The key secret is that the total sum of 1+3+5+…+the nth odd number

always equals n squared exactly. Since 2025 = 2 x 1013 – 1, we can know that 2025 is the 1013th odd number. So, 1+3+5+…+2023+2025 must equal exactly 1013 squared. Taking the square root leaves us with 1013 in honour of 13-year-old Rishi (to whom I awarded 10 points) 🙌😊

Chess Helpmate Puzzle

A delightful Chess puzzle which I saw posted on Facebook recently.

It’s Black to play and co-operate fully in a Helpmate in six moves! That is, Black starts a co-operative sequence which ends with White delivering checkmate on his 6th move. Can you do as well as Problem-Solving Chess Grandmaster Dolf Wissmann by cracking the puzzle in under a minute!? 👌

Solution:

Once we realise that the required end-position is this one, it becomes much easier to figure out that it can be reached from the puzzle’s starting position via the sequence
1…g5 2 Kf2 g4 3 Ke3 g3 4 Kd4 g2 5 Kxd5 g1=B 6 Kc6 Ba7 7 Kc7#

Bonus Two-Part Fantasy Chess Puzzle 💕

What is the maximum number of rooks which can be placed on an empty Chess board such that none of them are attacking each other?
What is the maximum number of knights which can be placed on an empty Chess board such that none of them are attacking each other?

Answers

Eight rooks, placed on a common long diagonal of a Chess board, will not be attacking each other.
32 knights, either all on dark squares or all on light squares, will not be attacking each other.

Happy New Year Wishes from Paul, Jenny & Michael Motwani ❤️❤️❤️

A Happy New Year Trigonometry Puzzle In Honour of

Chief Arbiter Erwin Denissen, who is also a Mathematics Teacher

Photo by Bart Beijer of Erwin Denissen & Harry Gielen 👍👍

Without needing to use a calculator or any other external aids, figure out mentally the exact value of the square root of sin 2025° * cos 2025° * tan 2025°

Answer:

sin x° * cos x° * tan x° = sin x° * cos x° * (sin x° ÷ cos x°) = (sin x°) squared, and so its square root will be the absolute value of sin x°.

sin 2025° = sin (5 x 360 + 225)° = sin 225° = -sin 45° = -1/sqrt 2.

Its absolute value is 1/sqrt 2 or equivalently (sqrt 2) ÷ 2.

Another Sneaky Square Root Surprise!

Think about the square root of 2025. What surprise do we get if we increase each digit of 2025 by 1 and then take the square root?

Answer: The square root of 2025 is 45. The square root of 3136 is 56. Both digits in the answer increased by 1, too! 😁

I will round off this article with one final nice photo and a beautiful, true quotation.

“You pay God a compliment by asking great things of Him”—St. Teresa of Avila 💕

Blog Post #169: Steps Towards Heaven 💕

Dear Readers,

I will begin by sharing that several very dear people (who were all really close to me for most of my life so far) passed on this year, but I believe with total certainty that we will later meet again in the Kingdom of Heaven.

If more people will come to know and truly believe that message of God’s greatest gift that He offers freely to all of us, then that will be a wonderful change. That is my biggest wish for Christmas 💕

In the past seven months or so, I received many beautiful messages from current or former Maths or Chess students or colleagues, I met lots of lovely people at Chess events in Temse (Belgium), Hull (England) and Lignano Sabbiadoro (Italy), and my wife and I got to share some very precious time in Scotland with the family of Paul Fitzpatrick (1948-2024, who was a fantastic teacher, friend and mentor to me for more than half a century) ❤️

This photo is from several years ago, at Paul’s home.
A happy high point of 2024 was the wedding of Michael Roy Fitzpatrick ❤️

Some of Paul’s children and grand-children are extremely good at Mathematics, as are a number of my current students and colleagues at Musica Mundi School (MMS) in Waterloo, Belgium. In honour of all of them, and Paul especially, I now offer the following fresh, original brainteaser, called ‘Steps Towards Heaven’ 💕

I estimate that I may have taken about 200000000 (two hundred million) steps in my life, so far. On a nice day out yesterday with my son, Michael, we comfortably did more than 10000 steps each. So, imagine 200000000 steps numbered individually 1, 2, 3,…and so on, up to 200000000 for my newest step!

Let’s say that Paul and I look back on them together. I pick one of the numbers, and Paul then multiplies it by one of the other numbers in the long list. We will note carefully the product result that we get from the multiplication.

Next, I pick one of the 199999998 numbers that has not yet been picked, and Paul multiplies it by one of the remaining numbers. We again note the product result carefully, and we continue like that until all the numbers have finally been chosen.

Our ‘Steps Towards Heaven’ Christmas Brainteaser for you is this: Can you figure out the absolute maximum total that can be obtained by adding up the one hundred million products that Paul and I will have noted?

You are wished very fine thoughts and lots of good fun too in solving the brainteaser. Please feel free to email me your best answers. Everyone who does so will be specially named and congratulated 👍👍 here in the New Year or possibly even sooner, God-willing as always.

In the meantime, warm congratulations are given right now to Hannah Hogstad, Wout Callens and Richard Riet (excellent students at MMS) and to Jens Van Steerteghem (my dear Maths colleague at the school), who all solved nice prize puzzles &/or brainteasers that I have been sharing with everyone at the school. Hannah and Jens will be receiving beautiful medals tomorrow, and Wout & Richard will be receiving other lovely gift prizes 👍😍

With love and kindest wishes,

Paul Motwani 💕😊

A St. Saviours High School Chess Club photo from the 1970s
with Miss Hazel Steele, Paul Fitzpatrick
my brother Joe, Paul Strachan, me and Kevin McGovern
after winning the Scotsman Chess Trophy 😍
I still love to think back over the myriad golden tips
(about Chess and Life in general)
that Paul generously gave me.
His wonderful wisdom continues to have a lasting positive effect ❤️

Blog Post #168: For Super Seinel, Lovely Laetitia and Brilliant Benjamin!!! 😊😊😊

Dear Friends,

Laetitia is a lovely lady chef at Musica Mundi School whose birthday is coming up on 28 May in just two days from now. Brilliant Benjamin is a student who’s had a great school year as a 16-year-old, and we’ll have special puzzles to celebrate him turning 17 this coming Wednesday 29th. I’m hoping for more solvers like Super Seinel who submitted the best answers to the most recent puzzles that I shared at the school. She will be receiving a very nice prize pen tomorrow. 👍😊

A Starter Puzzle in Honour of Laetitia’s Birthday on 28 May 😁

Use the numbers 2, 8, 2, 8, 2 in any order you like in a calculation to get the result 28. You can use operations involving +, -, x, ÷, ( ) as you wish.

Benjamin is about to turn 17. Let’s note that 17 = 8 + 9, and 17² = 289.

A Warming-Up Puzzle in Honour of Benjamin

In how many years from now will be the next (future) time that the square of Benjamin’s age then will end with the digits 89 on the right? 👌

As Brilliant Benjamin always gave 100% top efforts in my Maths class at the school, here comes…

A Modest Brainteaser in Honour of Benjamin here in Blog Post # 24+24+24+24+24+24+24 😍

Part 1: I’m thinking of a particular number. If I add 2400 to the number, then its square root increases by exactly 16 (compared to the square root of the original starting number).

What number was I thinking of at the start?

Part 2: I am currently 61 years old. When can be the soonest (future) time that the square of my age then would end with the digits 89 on the right? Could there be yet another such time later on? 🙌

Part 3: In Heaven, the good and joyful events will truly be infinite. As a sample taster, imagine a special feast of 289 celebrations there. Several celebrations before celebration #289, an angel announces that the square of that particular celebration number gives a number ending with the digits 89 on the right.

Given that information, and without even needing to use a calculator, deduce the exact celebration number when the angel’s announcement is made. ❤️

I saw this beautiful photo via the Facebook page of a friend named Antonio
who posts really good and inspirational messages every day 👌💕

A Puzzle in Honour of Super Seinel 😊

Seinel’s birthday is not tomorrow! However, tomorrow it will be 41 days since her birthday, and we can still have some good Maths fun with that…!!

Think of any friend who’s less than 40 years old! Multiply their current age by the age they’ll be on their next birthday. Now add on the magic number 41.

What do you notice that’s special about all the results that can be obtained like that!?

A Nice Word Puzzle involving Seinel’s Prize Pen 👍😊

Rearrange the letters of SUPER SEINEL to make the word PENS + a proper seven-letter English word.

I wish you oodles of enjoyment with all the puzzles 😁, and please do feel free to send me your solutions by email, if you like. 👍

With kindest wishes as always,

Paul M😊twani ❤️

I’ll conclude this Blog Post #168 with the beautiful Bible Psalm 16:8

“I have set the LORD always before me; because He is at my right hand, I shall not be shaken.”

Blog Post #167: Fifty Years of Great Chess Friendships 💕😊

Dear Friends,

In the past fifty years since I was first introduced to the Royal Game of Chess at the age of 11 in Scotland, I can truly say with gratitude that I have met thousands of lovely people through the beautiful game. I still remember many of the moves that were played, but I remember the people much more!

Even if one can’t always personally let everyone know that they are very fondly thought of and remembered, there’s no better time than the present to let people know we care. 💕

This photo from 30 years ago–way back in 1994!–is one of my favourites 😍.
Jenny (whom I married soon after) is pictured with Harald Fietz,
Ian Grant and Jonathan Grant, whose birthday is coming up in just a few days from now 😊.

***Andrée Upton-Regnier’s birthday is coming soon too, A days after Jonathan Grant’s birthday…***😊

***The birthday of Woman Chess Grandmaster Erika Sziva is also coming soon,***
*in early June, exactly Ax3 days from today…*😁

Early Birthday Puzzle in Honour of Chess Friends Jonathan Grant, Andrée Upton-Regnier & Erika Sziva ❤️

Today (May 18) is day number 139 of this year 2024. So, Jonathan’s birthday coming up will be on day number J of this year, where J is clearly greater than 139. Andrée’s birthday will be A days after Jonathan’s, where J x A = 1001. Also, Erika’s birthday will be A x 3 days from today.

Your fun puzzle is to figure out the exact dates (month & day number) of the birthdays of Jonathan, Andrée and Erika. 👍👌🙌

Some of my dear friends have passed on, but they will never be forgotten either ❤️

This photo from January 1979 includes me with great school friends
Shaun, Mike P., Andrew, Gary, Tony, Mike H., Mike D. and Martin.
Martin Jackson and Tony Welsh have passed on, but will always be remembered fondly ❤️

A Chess photo from 1982
with dear friends Tim Upton (19.12.1958-10.1.2018) and Graham Morrison (10.11.1958-13.5.2024).
Graham was Scottish Champion in 1981, and represented Scotland frequently
at international level, playing in Olympiads in 1984, 1988, 2010 & 2012,
and in many European Team Championships.
He was also a long-standing player in the 4NCL, formerly with Barbican before moving to Alba.
I had been very much looking forward to seeing Graham at the British Chess Championships
this summer, as he had also signed up to take part.
He was a really lovely, kind and gentle man ❤️
who will be missed greatly by all who knew him well.
Sincere condolences and thoughts go to Graham’s wife, Lynne.

This position, with ***White to play and win***,
is based on a game of Graham’s from the 1989 Edinburgh Open, 35 years ago!
Graham loved to have the bishop pair in Chess, and he frequently used it to great effect.
Enjoy finding the strongest directly-winning idea, just like FIDE Master Graham Morrison did! 😍

Look closely at this photo from way back in 1990…
In the foreground is FIDE Master Donald Holmes playing Black
against a remarkable boy who was later to become an International Grandmaster.
Happy birthday wishes for tomorrow to GM Jonathan Parker! ❤️😊

Super-Fast Puzzle in Honour of Jonathan Parker 😁

What age will Jonathan be turning tomorrow (on 19.5.2024) if I tell you that then half of his life so far will have been in the 21st century, while the first half (so far) was in the 20th century?

In the photo above from Musica Mundi School, the boy playing me is Aimar,
and there he’s the same age that Jonathan Parker turned in 1990,
a few years before he became a Chess Grandmaster…

Happy Birthday Wishes to Aimar for tomorrow, too!! ❤️😁

A fun photo at the Musica Mundi School Chess Club ❤️

Fun Puzzle for Aimar’s Birthday tomorrow (19 May) 😊

In this puzzle, we’ll make good use of several nice numbers 👍😁

We’ll use 160, the total number of Chess pieces and pawns that were on the five boards (in the photo above) at the very start of the games.

We’ll also use 10 (the number of people pictured playing), and 3 (my favourite number) and 8 (the number of letters in BIRTHDAY). Note that sqrt stands for “the square root of” in Aimar’s Birthday calculation ❤️

Calculate 3 ÷ 8 * sqrt (160*10) to verify the age that Aimar will be on his birthday tomorrow 😍

I was invited recently to do a ‘simultaneous exhibition’, playing more than 20 Chess members and friends of Boey-Temse Chess Club, celebrating the thriving club’s first 50 years (1974-2024). I would like to specially thank Marc Blommaert (Club Chairman/President) for the wonderful invitation; Luc De Ryck (former long-time Mayor of Temse) for his delightful speech; Wim Van Rossen (Alderman and prominent board member of ‘Gemeente Temse’) for his very thoughtful words and generous gift too ❤️.

Many of the photos are published with the kind permission of professional photographer Julien Heerwegh, while others were sent to me by Rita Ysewyn, Geert Vanstraelen, Geert Wille, Bart Vereecken, Marc De Meireleir and Marc Blommaert. (I have saved some photos for future occasions 😊.)

In the Chess games with Willem Verrijdt, Wiebke Barbier, Rudy Van Laeken, Kurt De Maeyer, Luc De Ryck, Robin Blommaert, Jonas De Bock, Emiel Slachmuylders, Loic Verbeke, Bjorn Dijckmans, Gust Van Der Meiren, Hugo Stuer, Geert Wille, Marc Blommaert, Marcel Wynants, Steven Lippens, Geert Vanstraelen, Luc Vereecken, Wim Van Rossen, Wim Barbier and Pascal Kegels, everyone fought well, and Pascal got a draw…and very nearly more! It was a great pleasure for me to give prizes for everyone. (Felix Verelst was also going to play, but hopefully we’ll meet at a future celebration.)

The final game to finish was the one with Bjorn Dijckmans, after 6 hours of play!!

I enjoy great movies as much as Chess! One of my absolute favourite pieces of film music was John Barry’s “Dawn Raid on Fort Knox” from 60 years ago in the 1964 James Bond “Goldfinger” 👌❤️

https://www.youtube.com/watch?v=nnW-8YpQpgQ (5 minutes 48 seconds).

I was reminded of it by a game in the ‘simul’ which reached the following position from the Fort Knox variation of the French Defence…

One of the brilliant mathematicians who played against me in the ‘simul’ was Robin Blommaert, son of Marc Blommaert. Their birthdays are both in July, but I’ll be seeing them sooner, this month. For their enjoyment–and hopefully yours too!!–I decided to compose a couple of nice puzzles in which I’m also thinking of Harriet, a dear colleague whose birthday was/is this month, and my wife Jenny who’s turning 56 next month.

Fun Puzzle in Honour of Harriet and Jenny! 💕

I saw a great film one day in April. The ‘Film day’ number F was of course something between 1 and 30 inclusive. The day number H of Harriet’s birthday in May was/is of course something between 1 and 31 inclusive. If I add up F and H and also the number of days from the Film day until Harriet’s birthday, the result is 56.

Your fun puzzle is now to figure out the exact day number in May of Harriet’s birthday! 😍

B😊nus Fun Puzzle in Honour of my youngest sister & her husband (my brother-in-law) 😊❤️

My youngest sister and her husband recently celebrated their Silver Wedding Anniversary and their birthdays too.

For simplicity in this puzzle, let’s suppose that their birthdays are on the same day as each other (same month and day number).

We’ll say that S is my sister’s age and B is my brother-in-law’s age.

Imagine calculating their sum, their difference, and their product too. Then calculate the total sum T of all of that!

I will tell you honestly that, in their case, T is always a square number, every year.

Your fun puzzle is now to figure out the age difference (in years) of my sister and her husband. 🙌💕

Word Puzzle

Rearrange the letters of LEGACY IN SUN to make a proper 11-letter English word which describes how God loves us all.

I’ve in general been so busy for quite a long time that I must soon catch up a bit with publishing solutions to various puzzles in certain previous articles, but in the meantime I wish you oodles of enjoyment with all the puzzles 😁, and please do feel free to send me your solutions by email, if you like. 👍

With kindest wishes as always,

Paul M😊twani ❤️

I’ll conclude this Blog Post #167 with the beautiful Bible Psalm 67:1